SHTns also provides vector transforms.

Radial - Spheroidal - Toroidal decomposition

The components of a vector field on a sphere 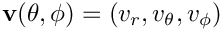$\mathbf{v}(\theta,\phi) = (v_r, v_\theta, v_\phi)$ in canonical spherical coordinates cannot be transformed as scalars, because they do not behave like scalar fields under rotation for example (actually only the radial component does).

To overcome this, we use the following decomposition:

$\mathbf{v} = Q(\theta,\phi) \mathbf{e_r}+ r \nabla S(\theta,\phi) - \mathbf{r} \times \nabla T(\theta,\phi)$

where Q, S and T are respectively the radial, spheroidal and toroidal scalar fields. We have explicitely:

$\mathbf{v} = \left( \begin{array}{rcl} Q & & \\ \partial_\theta S & + & \frac{1}{\sin\theta} \partial_\phi T \\ \frac{1}{\sin\theta} \partial_\phi S & - &\partial_\theta T \end{array} \right)$

Expanding Q, S and T (which are scalar fields) in spherical harmonics gives:

$\mathbf{v} = \sum_{l,m} \left( Q_l^m \, Y_l^m(\theta,\phi) \mathbf{e_r}+ S_l^m \, r \nabla Y_l^m(\theta,\phi) - T_l^m \, \mathbf{r} \times \nabla Y_l^m(\theta,\phi) \right)$

If this only involves a simple scalar transform for the radial component, it does involve derivatives of spherical harmonics for the tangential components.

The functions SHqst_to_spat and spat_to_SHqst transform vector fields from their spherical coordinate spatial representation Vr, Vt, Vp to their spectral representation using Qlm, Slm and Tlm.

The functions SHsphtor_to_spat and spat_to_SHsphtor do the same for a tangential vector on the sphere (without radial component).

See also: A closely related definition of vector spherical harmonics on wikipedia.

Note: The energy of the vector field can be retrieved from it's orthonormal spherical harmonic representation as:
$\int ||\mathbf{v}||^2 = \sum_{l,m \geq 0} C_m N_l \: \left( |Q_l^m|^2 \, + \, l(l+1)\,\left( |S_l^m|^2 + |T_l^m|^2 \right) \right)$
where and are defined in the Energy section.

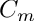
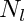
Special case of 3D divergence-free fields

For a divergenceless 3D vector, the radial scalar Q and the spheroidal scalar S can be derived from the same poloidal scalar P :

$Q = \frac{l(l+1)}{r} P$

$S = \frac{1}{r} \frac{\partial \, rP}{\partial r}$

which corresponds to the poloidal/toroidal decomposition that ensures the vector field to be divergence-free.

$\mathbf{v} = \nabla \times (T \mathbf{r}) + \nabla \times \nabla \times (P \mathbf{r})$