Spherical Harmonic coefficients layout

The field A is decomposed on the basis of spherical harmonics Ylm (degree l, order m) :

$A(\theta,\phi) = \sum_{l,m} A_l^m Y_l^m(\theta,\phi)$

The series is truncated at degree LMAX and order MMAX*MRES, and only order that are multiple of MRES are described.

For real-valued spatial data A

The collection of Alm (spherical harmonics coefficient of degree l and order m) is stored in an array of complex double floating point values. The spherical harmonic truncation is defined by a call to shtns_init or to shtns_create which returns an shtns_cfg object (pointer to shtns_info) from which the the size of the array, shtns_info::nlm, can be read (see examples).

The NLM coefficients Alm are stored in a one-dimensional array, grouped by m.
The details of the storage may depend on the algorithm, and to access a particular coefficient, you should always use the following macros :

From C

LM(shtns, l,m) gives the index in the array for coefficient of degree l and order m.
LiM(shtns l,im) gives the index in the array for coefficient of degree l and order im*MRES.

Hence Alm[LM(shtns,l,m)] is the (complex) SH coefficient of degree l and order m.

From Fortran

call shtns_lmidx(lm, l, m), will return the index lm for degree l and order m

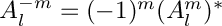
Note: For real spatial data, the Spherical Harmonic coefficients with negative m are related to the complex conjugate of the positive m coefficients : $A_l^{-m} = (-1)^{m} (A_l^m)^*$ . For efficiency purposes, only the coefficients with positive m are stored.; There is no test on bounds, so that LM(shtns, l,m) with l or m that is not described, will give undefined result (in particular for an m that is not a multiple of MRES)

To perform loops on all coefficients, use the macros LM_LOOP and LM_L_LOOP in combination of the arrays shtns_info::li which give the degree l and functions of it for any array index.

For complex-valued spatial data

Complex spatial data can be transformed using spat_cplx_to_SH and SH_to_spat_cplx The indexing of the spectral coefficients in Alm is then different from the real-valued data. In addition, all l and m are present. Indeed to access coefficient of degree l and m, we use

Alm[l*(l+1)+m]

or

Alm(l*(l+1)+m+1)

from C or Fortran respectively.

Allocation

Allocation for a SH description is simply done with :

Alm = fftw_malloc( NLM * sizeof(complex double) );

The use of fftw_malloc ensures proper alignment of data for SSE vectorization (if fftw has been properly compiled with –enable-sse2 or –enable-avx).

Normalization

Several normalizations for the spherical harmonics exist (details on wikipedia). SHTns lets you choose one of the following :

Orthonormalized is the default (also used in the GSL)

$Y_l^m(\theta, \phi) = \sqrt{\frac{2l+1}{4\pi}} \sqrt{\frac{(l-m)!}{(l+m)!}} \, P_l^m(\cos \theta) \, \exp(im\phi)$
Four-pi normalized

$Y_l^m(\theta, \phi) = \sqrt{2l+1} \sqrt{\frac{(l-m)!}{(l+m)!}} \, P_l^m(\cos \theta) \, \exp(im\phi)$
Schmidt semi-normalized

$Y_l^m(\theta, \phi) = \sqrt{\frac{(l-m)!}{(l+m)!}} \, P_l^m(\cos \theta) \, \exp(im\phi)$

shtns_init uses the default (defined by SHT_DEFAULT_NORM) but you can choose another normalization by calling shtns_create instead.

The Legendre associated functions are defined by :

$P_l^m (x) = (-1)^m\ (1-x^2)^{m/2}\ \frac{d^m}{dx^m}P_l(x)$

which includes the Condon-Shortley phase 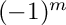by default.

For reference, function SH_to_point gives a simple explicit implementation of the inverse SH transform (synthesis).

Normalization variations

Use shtns_create with SHT_NO_CS_PHASE to disable the Condon-Shortley phase. For example, to initialize a Schmidt semi-normalized transform of maximum degree 16 without Condon-Shortrley phase, use

shtns_create(16, 16, 1, sht_schmidt | SHT_NO_CS_PHASE);

shtns_create

shtns_cfg shtns_create(int lmax, int mmax, int mres, enum shtns_norm norm)

Defines the sizes of the spectral description. Use for advanced initialization.

Definition sht_init.c:1100

SHT_NO_CS_PHASE

#define SHT_NO_CS_PHASE

don't include Condon-Shortley phase (add to last argument of shtns_create)

Definition shtns.h:53

sht_schmidt

@ sht_schmidt

Schmidt semi-normalized : 4.pi/(2l+1)

Definition shtns.h:50

By default, SHTns uses "complex" spherical harmonic normalization. However, as it deals only with real functions, the m<0 coefficients are not stored, since they are complex conjugate of the m>0 ones. Thus, one must pay attention, that the m>0 coefficient have to be counted twice in a total energy calculation.

An alternative to this "complex" normalization is the "real" normalization, for which the energy is simply the sum of the coefficients (m>=0) squared. Use shtns_create with SHT_REAL_NORM to use a "real" spherical harmonic normalization. This is the usual "real" spherical harmonics, if one takes the complex conjugate of the coefficients.

A few useful examples, for orthonormal spherical harmonics :

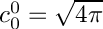
a constant unit value on the sphere is represented by the coefficient $c_0^0 = \sqrt{4\pi}$ .
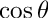
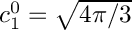
$\cos \theta$ is represented by the coefficient $c_1^0 = \sqrt{4\pi/3}$ .
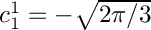
$\sin \theta \, \cos \phi$ is represented by $c_1^1 = -\sqrt{2\pi/3}$ (with Condon-Shortley phase)
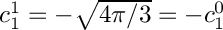
with a "real" normalization instead, one would have $c_1^1 = -\sqrt{4\pi/3} = -c_1^0$ .

The functions sh00_1(), sh10_ct(), sh11_st() shlm_e1() will help to build simple spectral fields, no matter what normalization you choose.

Energy

Note

The energy of a scalar field can be retrieved from it's spherical harmonic representation as:

$\int ||q||^2 = \sum_{l,m \geq 0} C_m N_l \: |Q_l^m|^2$

where

and

are the following normalization factor:

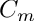
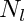
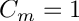
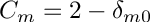
if SHT_REAL_NORM has been used, . Otherwise $C_m = 2 - \delta_{m0}$ (ie for and for ).
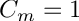
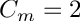
for sht_orthonormal :
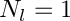
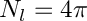
for sht_fourpi : $N_l = 4\pi$
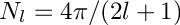
for sht_schmidt : $N_l = 4\pi/(2l+1)$

Troubleshooting

If you have problems in getting your spherical harmonic coefficient right, you may check the following :

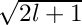
Schmidt semi-normalization ? try multiplying or dividing by $\sqrt{2l+1}$
Condon-Shortley phase ? try multiplying by
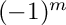
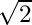
Real or Complex ? try multiplying or dividing the m>0 coefficients by $\sqrt{2}$
Relative sign ? try to take the complex conjugate of the coefficients.
Does the array include l=0 ?