Chapter 1 Getting started
1.1 Description
XSHELLS is yet another code simulating incompressible fluids in a spherical cavity. In addition to the Navier-Stokes equation with an optional Coriolis force, it can also time-step the coupled induction equation for MHD (with imposed magnetic field or in a dynamo regime), as well as the temperature (and concentration) equation in the Boussinesq framework.
XSHELLS uses finite differences (second order) in the radial direction and spherical harmonic decomposition (pseudo-spectral). The time-stepping uses a highly stable, second order, semi-implicit, predictor-corrector scheme (with only diffusive terms treated implicitly).
XSHELLS is written in C++ and designed for speed. It uses the blazingly fast spherical harmonic transform library SHTns, as well as hybrid parallelization using OpenMP and/or MPI. This allows it to run efficiently on your laptop or on parallel supercomputers. A post-processing program is provided to extract useful data and export fields to python/matplotlib or paraview.
XSHELLS is free software, distributed under the CeCILL Licence (compatible with GNU GPL): everybody is free to use, modify and contribute to the code.
1.2 Easy installation
Grab the XSHELLS archive and extract it. Alternativley, you can use git to clone the repository
git clone --recurse-submodules https://bitbucket.org/nschaeff/xshells.git
1.3 Manual installation
If you need to install XSHELLS manually (e.g. because the above easy installation fails or you need a specific configuration not covered by the wizard), here are some useful details.
1.3.1 Requirements
The following items are required:
-
•
a Unix like system (like linux),
-
•
a C++ compiler,
-
•
the FFTW library, or the intel MKL library.
-
•
the SHTns library, which is included as a git submodule.
The following items are recommended, but not mandatory:
-
•
either g++ or clang++ compiler 11 1 The intel compiler should also work, but some vendor compilers have been reported to fail to compile, or even worse, lead to wrong/unreproducible results at runtime.
-
•
an MPI library (with thread support),
-
•
the HDF5 library for post-processing and interfacing with paraview,
-
•
Python 3, with NumPy and matplotlib (Python 2.7 should also work),
-
•
Gnuplot, for real-time plotting.
-
•
EVTK, for converting slices to VTK format for paraview.
1.3.2 Installing FFTW
FFTW (or the intel MKL) library must be installed first. FFTW comes already installed on many systems, but in order to get high performance, you should install it yourself, and use the optimization options that correspond to your machine (e.g. --enable-avx). Please refer to the FFTW installation guide.
Note that it is possible to use the intel MKL library instead of FFTW. To do so, you must configure XSHELLS (and SHTns if you configure it separately) with the --enable-mkl option.
1.3.3 Configuring XSHELLS
Get the XSHELLS archive and extract it. Alternativley, you can use git to clone the repository
git clone --recurse-submodules https://bitbucket.org/nschaeff/xshells.git
From the XSHELLS source directory, run:
./configure
to automatically configure XSHELLS for your machine. This will also automatically configure SHTns and compile it. Type ./configure --help to see available options, among which --disable-openmp and --disable-mpi, but also --enable-mkl to use the intel MKL library instead of FFTW.
Before compiling, you need to setup the xshells.hpp configuration file (see next section). To check that everything works, you may also want to run the tests, with python test.py or equivalently make test.
1.4 Configuration files
There are two configuration files:
-
•
xshells.hpp is read by the compiler (compile-time options), and modifying it requires to recompile the program. The corresponding options are detailed in section 2.2.
-
•
xshells.par is read by the program at startup (runtime options) and modifying it does not require to recompile the program. This file is detailed in section 2.1.
See chapter 2 for more details. Example configuration files can be found in the problems directory.
Before compiling, copy the configuration files that correspond most closely to your problem. For example, the geodynamo benchmark:
cp problems/geodynamo/xshells.par . cp problems/geodynamo/xshells.hpp .
and then edit them to adjust the parameters (see sections 2.2 and 2.1).
1.4.1 Transition from versions 1.x to 2.x
Due to the change of time-stepping scheme, in xshells.par:
-
•
adjust time-steps (x3 to x4)
-
•
adjust constants for variable time-step
Due to internal changes, in xshells.hpp:
-
•
some variables have their name changed. see examples.
Slices written by xspp are now in Numpy format (instead of text format). As a consequence, matlab/octave display scripts have been dropped.
1.5 Compiling and Running
When you have properly set the xshells.hpp and xshells.par files, you can compile and run in different flavours:
Parallel execution using OpenMP with as many threads as processors (recommended for laptops or for running on small servers):
make xsbig ./xsbig
Parallel execution using OpenMP with (e.g.) 4 threads:
make xsbig OMP_NUM_THREADS=4 ./xsbig
Parallel execution using MPI with (e.g.) 4 processes:
make xsbig_mpi mpirun -n 4 ./xsbig_mpi
Parallel execution using OpenMP and MPI simultaneously (hybrid parallelization), with (e.g.) 2 processes and 4 threads per process:
make xsbig_hyb OMP_NUM_THREADS=4 mpirun -n 2 ./xsbig_hyb
Parallel execution using MPI in the radial direction and OpenMP in the angular direction, with (e.g.) 16 processes and 8 threads per process:
make xsbig_hyb2 OMP_NUM_THREADS=8 mpirun -n 16 ./xsbig_hyb2
Note that xsbig_hyb2 requires the OpenMP-enabled SHTns (./configure --enable-openmp)
Batch schedulers
Some examples for various batch schedulers and super-computers are also available in the batch folder.
1.6 Outputs
All output files are suffixed by the job name as file extension, denoted job in the following. The various output files are:
-
•
xshells.par.job : a copy of the input parameter file xshells.par, for future reference.
-
•
xshells.hpp.job : a stripped-out version of the file xshells.hpp that was used during compilation, for future reference.
-
•
energy.job : a record of energies and other custom diagnostics. Each line of this text file is an iteration.
-
•
fieldX0.job : the imposed (constant) field X, if any.
-
•
fieldX_####.job : the field X at iteration number ####, if parameter movie was set to a non-zero value in xshells.par.
-
•
fieldXavg_####.job : the field X averaged between previous iteration and iteration number ####, if parameter movie was set to 2 in xshells.par.
-
•
fieldX.job : the last full backup of field X, or field X at the end of the simulation. Used when restarting a job.
All field files are binary format files storing the spherical harmonic coefficients of the field. To produce plots and visualizations, they can be post-processed using the xspp program (see chapter 3).
1.7 Limitations and advice for parallel execution
The parallelization of XSHELLS is done by domain decomposition in the radial direction only, using MPI. In addition to this domain decomposition, shared memory parallelism is implemented using OpenMP. Furthermore, MPI-3 shared memory can be used for communications between processes on the same node, with significant performance gains, and somehow mimicking a two-dimensional domain decomposition. The MPI-3 shared memory solver in XSHELLS requires a cache-coherent architecture, and is currently enabled by default only on x86 machines. To enable or tune MPI-3 shared memory, add -shared_mem=N to the command line, with N the number of cores that should share memory.
There are four variants of the code that differ in the way OpenMP is used:
-
•
xsbig uses only OpenMP in the radial direction (no MPI). It can only run on a single node, but does not need an MPI library. This is good for a general purpose desktop or laptop computer, but also on NUMA nodes (although some MPI may lead to better performance). Low memory usage.
-
•
xsbig_mpi uses only MPI in the radial direction (no OpenMP). This is good for medium sized problems, running on small clusters.
-
•
xsbig_hyb uses both MPI and OpenMP in the radial direction, to reduce the number of MPI processes and memory usage. As a consequence, it is more efficient to use a number of radial shells that is a multiple of the number of computing cores. Beyond 1 thread per radial shell (or in case of imbalance), OpenMP tasks are used to share the work of one shell across several threads, although this leads to a less than ideal scaling.
-
•
xsbig_hyb2 uses MPI in the radial direction and OpenMP within a radial shell. This strategy usually performs well, allows to efficiently address more computing cores, but uses a lot of memory (an order of magnitude more than xsbig_hyb). It is highly recommended to use a number of radial shells that is a multiple of the number of nodes. This mode cannot go beyond 1 MPI process per radial shell, but intra-node shared memory parallelism allows to use all cores of a single node within each process. Note also that the SHTns library compiled with OpenMP is needed.
In any case, the number of MPI processes cannot exceed the total number of radial shells. It is often more efficient to use a small number of MPI processes per node (1 to 4) and use OpenMP to have a total number of threads equal to the number of cores.
Because there is no automatic load balancing, some situations where the same amount of work is not required for each radial shell will result in suboptimal scaling when the number of MPI processes is increased. Such situations include (i) solid conducting shells (e.g. a conducting inner core) and (ii) variable spherical harmonic degree truncation (e.g. in a full-sphere problem). In these cases, especially the latter, use pure OpenMP or minimize the number of MPI processes.
Using MPI executables (including hybrid MPI+OpenMP) is thus optimal only if the following conditions are both met:
-
•
all fields span the same radial domain (no conducting solid shells);
-
•
the radial domain does not include the center (and XS_VAR_LTR is not used, see section 2.2.3).
In such cases, XSHELLS should scale very well up to the limit of 1 thread per radial shell, and even beyond with the in-shell OpenMP mode of xsbig_hyb2 (see scaling example in Figure 1.1).
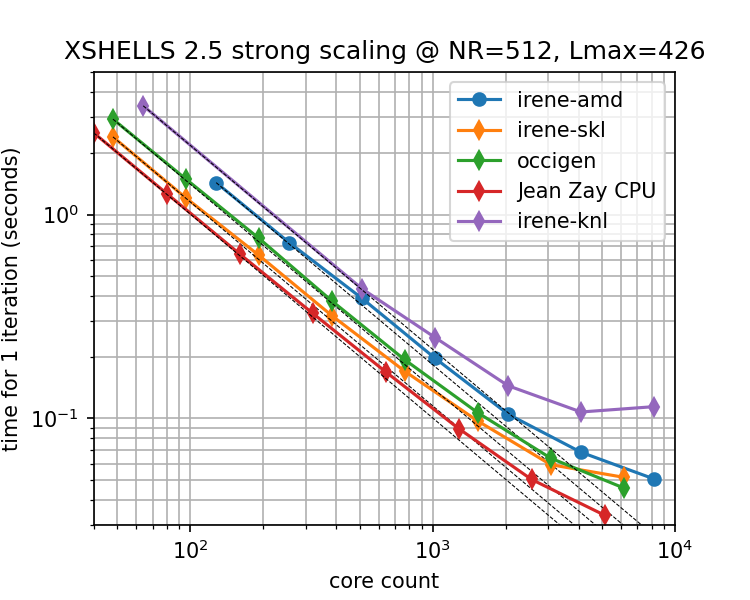
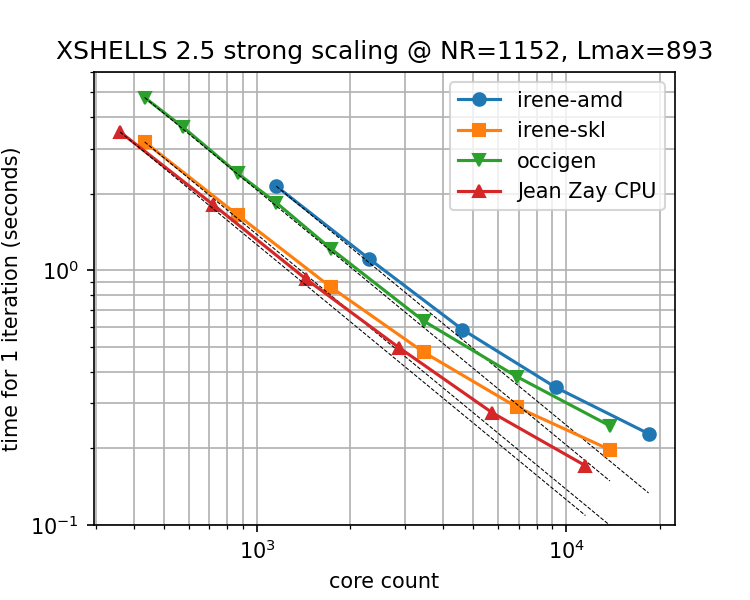
Advice for various hardwares:
-
•
Intel servers (Xeon): Best performance is usually obtained with 1 or 2 MPI processes per socket. Tuning the use of MPI-3 shared-memory across one socket or one node may be useful. Add -shared_mem=N to the command line, where N is the number of cores of each CPU (socket) or each node. Using shared-memory across a whole node may help scaling to larger core counts, but can reduce raw performance (depending on machines).
-
•
AMD Epyc 2nd generation (Rome): 4 OpenMP threads should give the best performance. Hence, one should use xsbig_hyb or xsbig_hyb2 with a number of MPI processes 4 times less the number of physical cores.
-
•
AMD Epyc 3rd generation (Milan): 8 OpenMP threads (but 4 on some machines) should give the best performance. Hence, one should use xsbig_hyb or xsbig_hyb2 with a number of MPI processes 8 times (4 times) less the number of physical cores.
1.8 Citing
If you use XSHELLS for research work, you should cite the SHTns paper (because the high performance of XSHELLS is mostly due to the blazingly fast spherical harmonic transform provided by SHTns):
N. Schaeffer, Efficient Spherical Harmonic Transforms aimed at pseudo-spectral numerical simulations, Geochem. Geophys. Geosyst. 14, 751-758, doi:10.1002/ggge.20071 (2013)
In addition, depending on the problem you solve, you could cite:
-
•
Geodynamo:
N. Schaeffer et. al, Turbulent geodynamo simulations: a leap towards Earth’s core, Geophys. J. Int. doi:10.1093/gji/ggx265 (2017) -
•
Spherical Couette:
A. Figueroa et. al, Modes and instabilities in magnetized spherical Couette flow, J. Fluid Mech. doi:10.1017/jfm.2012.551 (2013) -
•
Full-spheres: E. Kaplan et. al, Subcritical thermal convection of liquid metals in a rapidly rotating sphere, Phys. Res. Lett. doi:10.1103/PhysRevLett.119.094501 (2017)
-
•
Kinematic dynamos:
N. Schaeffer et. al, Can Core Flows inferred from Geomagnetic Field Models explain the Earth’s Dynamo ?, Geophys. J. Int. doi:10.1093/gji/ggv488 (2016)