The angular coordinates on a spherical shell are the co-latitude 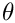$\theta$ and the longitude $\phi$ .

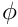
The spatial discretization is defined by a call to shtns_init; or to shtns_set_grid or shtns_set_grid_auto after shtns_create.

A field A (or one of its component in case of a vector field) is discretized on an ordered grid, which consists of

NPHI equally spaced nodes in longitude, spanning the range of angle between 0 (included) and $2\pi$ /MRES (excluded),
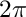
NLAT gauss nodes or equally spaced nodes (depending on shtns_type) in latitude, spanning angles from 0 to $\pi$ .

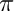
There are constraints on the sizes NLAT and NPHI. The sampling theorem requires NPHI > 2*MMAX, with MMAX the highest Fourier mode to be resolved. Similarly NLAT > LMAX is required for a Gauss-Legendre quadrature, while on a regular grid NLAT > 2*LMAX is needed for the Féjer and Clenshaw-Curtis quadratures.

When dealing with non-linear equations, or more generally when analysing data that is not band-limited to LMAX and/or MMAX, anti-aliasing constraints exist. For a given non-linear order of the equation N (typically 2 for a quadratic non-linear term), the anti-aliasing conditions are :

NPHI > (N+1)*MMAX
NLAT > (N+1)*LMAX/2 for Gauss-Legendre quadrature (Gauss nodes, non-equispaced).
NLAT > (N+1)*LMAX for Féjer or Clenshaw-Curtis quadratures (equispaced nodes).

Furthermore, the FFT is more efficient for certain values of NPHI and/or NLAT. If you do not require specific NLAT or NPHI, you can let SHTns choose them for you, by using shtns_set_grid_auto with nphi and/or nlat set to zero.

Identifying a grid point with its indices it and ip in latitudinal and longitudinal direction respectively (indices start at 0), one has :

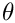
$\theta$ = acos(ct[it]) where ct = shtns_info::ct is initialized by the call to shtns_init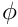
$\phi$ = ip * 2 $\pi$ /(NPHI*MRES) and PHI_RAD and PHI_DEG can be used to get the phi angle corresponding to ip.
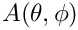
How to access $A(\theta,\phi)$ depends on the data layout, but it is always a contiguous array of double precision floating point values (64 bit)

Currently, three data layouts are supported. Contiguous longitudes, Contiguous latitudes, and Native layout.

Contiguous longitudes

In this layout, increasing longitudes are stored next to each other for each latitude. That is 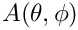$A(\theta,\phi)$ = A[it*NPHI + ip] in C or A(ip,it) in Fortran. Use SHT_PHI_CONTIGUOUS to instruct shtns_init to use this spatial data layout :

shtns_init ( sht_gauss | SHT_PHI_CONTIGUOUS, ... )

shtns_init

shtns_cfg shtns_init(enum shtns_type flags, int lmax, int mmax, int mres, int nlat, int nphi)

Simple initialization of the spherical harmonic transforms of given size. Calls shtns_create and shtn...

Definition sht_init.c:1583

SHT_PHI_CONTIGUOUS

#define SHT_PHI_CONTIGUOUS

use Contiguous longitudes

Definition shtns.h:68

sht_gauss

@ sht_gauss

use gaussian grid and quadrature. Allows on-the-fly or matrix-based algorithms.

Definition shtns.h:58

will tell shtns to precompute everything for a gauss grid, and spatial data stored with longitude varying fastest.

Contiguous latitudes

In this layout, increasing latitude are stored next to each other for each longitude. That is 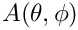$A(\theta,\phi)$ = A[ip*NLAT + it] in C or A(it,ip) in Fortran. Use SHT_THETA_CONTIGUOUS to instruct shtns_init to use this spatial data layout.

Additionally, SHT_ALLOW_PADDING instructs shtns to optimize the layout to avoid cache bank conflicts. This can lead to significant performance boost (from 1% to 50% depending on the architecture). In that case, shtns_info::nlat_padded > shtns_info::nlat and shtns_info::nspat > shtns_info::nlat * shtns_info::nphi to reflect the data layout.

Native layout

The "native" way of storing spatial field data will help you achieve the best performance with SHTns. On both CPU and GPU, it is the same as the Contiguous latitudes layout. Note that this may be subject to change and the data could be neither phi-contiguous nor theta-contiguous. For instance, in an earlier version (prior to v3.6), the GPU "native" layout was using the following access pattern: 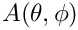$A(\theta,\phi)$ = A[ip*2 + (it%2) + (it/2)*(NPHI*2)] in C.

To instruct shtns_init that your spatial data has been set up using this layout, use SHT_NATIVE_LAYOUT.

Note: The safe way to allocate spatial data for all layouts is to use:
A = shtns_malloc( sh->nspat * sizeof(double) );

shtns_malloc
void * shtns_malloc(size_t bytes)
allocate appropriate CPU memory (pinned for gpu, aligned for avx, ...). Use shtns_free to free it.
Definition sht_init.c:1316; which will allocate the right amount of data and with optimal alignement.; In addition, it will allocate "pinned" memory when GPU support is enabled, for maximum transfer rate between GPU and CPU.; It is not recommended to use the native layout with Fortran or Python.