Speed
SHTns does not implement any "fast" algorithm. However, timings with other Spherical Harmonic Transform tools (including a fast algorithm) show that SHTns performs much faster than any other. Furthermore, even at large sizes, the fast algorithm we tested does not seem to be willing to take the lead.
Since v3.2, SHTns implements the new recurrence relation of Ishioka (2018), leading to faster transforms, especially for large transforms.
 | shtools 2.8 (Gauss) | libpsht (1 thread) | SpharmonicKit2 2.7 (fast) | SHTns 2.1 (1 thread, Gauss) | SpharmonicKit2/SHTns |
| 63 | 1.14 ms | 1.05 ms | 1.1 ms | 0.09 ms | 12.2 |
| 127 | 3.5 ms | 4.7 ms | 5.5 ms | 0.60 ms | 9.2 |
| 255 | 28 ms | 27 ms | 21 ms | 4.2 ms | 5.0 |
| 511 | 200 ms | 162 ms | 110 ms | 28 ms | 3.9 |
| 1023 | 1.8 s | 850 ms | 600 ms | 216 ms | 2.8 |
| 2047 | 13.0 s | 4.4 s | NA (out of memory) | 1.6 s | NA |
| 4095 | NA (seg fault) | 30.5 s | 11.8 s | NA |
Parallel speed
SHTns has parallel algorithms since version 2.2. When compared to libpsht (parallelized with OpenMP too), SHTns is faster especially for relatively small sizes.
| libpsht 20110131 | SHTns 2.2.1 | libpsht/SHTns |
| 63 | 5.0 ms | 0.05 ms | 100 |
| 127 | 5.4 ms | 0.22 ms | 24.5 |
| 255 | 8.5 ms | 1.4 ms | 6.1 |
| 511 | 23.5 ms | 6.5 ms | 3.6 |
| 1023 | 125 ms | 43 ms | 2.9 |
| 2047 | 700 ms | 331 ms | 2.1 |
| 4095 | 3.0 s | 2.0 s | 1.5 |
Accuracy
We claim that the accuracy of SHTns is as good as it can be with double precision floating point math. Rescaling is performed for large transform where the recurrence relation would otherwise underflow the double precision numbers. SHTns has been tested on x86 architecture with SSE2 double precision floating point math (64 bit) to be accurate up to l=16383 at least. The measured error for a back and forth scalar transform using a Gauss-Legendre algorithm for various truncation levels lmax is plotted below.
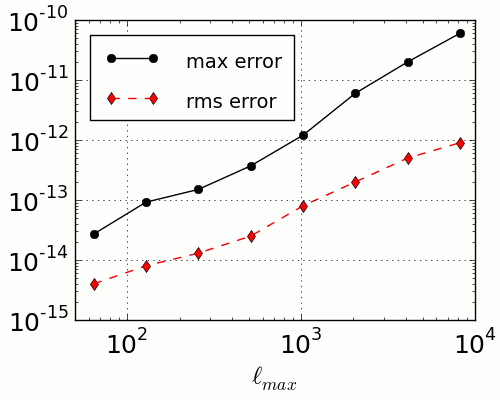
Don't trust our word, these results are obtained by running the time_SHT program, shipped with SHTns. For example :
